Расчет собственных векторов и собственных действий

Regular Matrix A =
Identity Matrix I =
Scalar Matrix(Z=c×I)
c =
|A| =
Singular Matrix (A - c×I) =
|A - c×I| =
Trace of A =
Eigen Value (c2) =
Eigen Value (c1) =
c1 in Eigen Vector x1 value =
c2 in Eigen Vector x1 value =
c1 in Eigen Vector x2 value =
c2 in Eigen Vector x2 value =

Собственный вектор квадратной матрицы A - ненулевой вектор V, когда A V = Λ V, λ называется собственным значением соответствия V.

Все собственные значения и собственные векторы удовлетворяют уравнению AX = λx для данной квадратной матрицы A.

Онлайн-эгенвекторы и калькулятор EigenValues ​​могут получить | a |, сингулярная матрица (A - C × I), след, исходное значение матрицы A

Например

Для матрицы

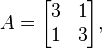
Вектор

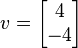
это собственник с собственным значением 2.

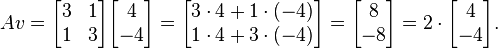
С другой стороны вектор

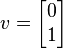
<я> не собственник, поскольку

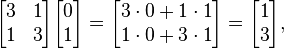
И этот вектор не является кратным исходным вектором V.

Расчет собственных векторов и собственных действий
Калькуляторы рекомендаций 12 часа до 24 часов преобразователя Разница времени и даты калькулятор Добавить / вычесть дни, месяцы и годы на сегодняшний день Калькулятор времени круга Количество будней калькулятора День рождения калькулятора недели Одолжил пасхальный воскресный календарь Онлайн добавление дней на сегодняшний день калькулятор Сотрудники ежегодный отпуск калькулятор Работа против жизненного стрессового баланса калькулятора День недели калькулятор Возраст калькулятора Дни в месяц, год калькулятор Конвертер дата календаря майя Дни между датами калькулятор