Стандартный отклонительный калькулятор

Enter Inputs	5,20,40,80,100 Enter the Numbers with Comma separated(,)

Result:
No.of Inputs
Mean
Standard Deviation(SD)
Population Standard Deviation(PSD)
Variance(SD)
Variance(PSD)
Calculation

Стандартный калькулятор отклонения для расчета общей меры распространения набора данных, это анализ данных. Калькулятор может дать вам количество входов, среднего, стандартного отклонения (SD), стандартное отклонение населения (PSD), дисперсию (SD), дисперсию (PSD) заданных входных значений набора данных.

Формула стандартного отклонения

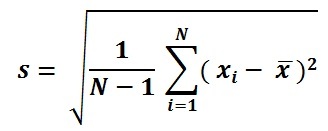
Standard Deviation Formula & Calculation

Население SD Формула

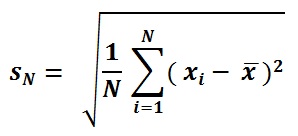
PSD - Population Standard Deviation Formula & Calculation

Формула дисперсии

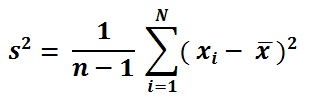
Variance Formula & Calculation

Средняя формула

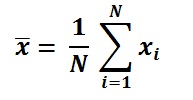
Mean Formula & Calculation

Например, когда дано набор данных 5,20,40,80,100 , результат будет:

.

Общие входы (N) = (5,20,40,80,100)

Всего входов (N) = 5

Значит (xm) = (x1 + x2 + x3 ... xn) / n

Значит (xm) = 245/5

Средства (xm) = 49

--------------------------------------------------

SD =

SQRT (1 / (N-1) * ((x1-xm) ^ 2 + (x2-xm) ^ 2 + .. + (xn-xm) ^ 2))

= SQRT (1 / (5-1) ((5-49) ^ 2 + (20-49) ^ 2 + (40-49) ^ 2 + (80-49) ^ 2 + (100-49) ^ 2 ))

= SQRT (1/4 ((- 44) ^ 2 + (- 29) ^ 2 + (- 9) ^ 2 + (31) ^ 2 + (51) ^ 2))

= SQRT (1/4 ((1936) + (841) + (81) + (961) + (2601)))

= SQRT (1605)

= 40.0625.

Дисперсия = SD ^ 2

Дисперсия = 40,0625 ^ 2

Дисперсия = 1605.

--------------------------------------------------

PSD =

SQRT (1 / (n) * ((x1-xm) ^ 2 + (x2-xm) ^ 2 + .. + (xn-xm) ^ 2))

= SQRT (1 / (5) ((5-49) ^ 2 + (20-49) ^ 2 + (40-49) ^ 2 + (80-49) ^ 2 + (100-49) ^ 2))

= SQRT (1/5 ((- 44) ^ 2 + (- 29) ^ 2 + (- 9) ^ 2 + (31) ^ 2 + (51) ^ 2))

= SQRT (1/5 ((1936) + (841) + (81) + (961) + (2601)))

= SQRT (1284)

= 35,8329

Дисперсия = SD ^ 2

Дисперсия = 35,8329 ^ 2

Дисперсия = 1284.

Стандартный отклонительный калькулятор

FoxCalculators - Бесплатные калькуляторы онлайн!